Question

Solve the following equation on the interval [0°, 360º). Round answers to the nearest tenth. If there is no solution, indicate "No Solution."-9cos(x) = 12sec(x) - 21

Answer 1

we have the equation

`-9\cos x=12\sec x-21`

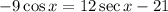
Rewrite

`-9\cos x=(12)/(\cos x)-21`

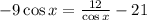
Multiply both sides by cosx

`-9\cos x\cdot\cos x=\cos x\cdot(12)/(\cos x)-21\cdot\cos x`
`\begin{gathered} -9\cos ^2x=12-21\cos x \\ -9\cos ^2x+21\cos x-12=0 \end{gathered}`

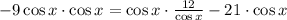
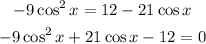
Change the variable

u=cosx

substitute

`-9u^2+21u-12=0`

Solve the quadratic equation

using the formula

a=-9

b=21

c=-12

substitute

`u=\frac{-21\pm\sqrt[]{21^2-4(-9)(-12)}}{2(-9)}`
`\begin{gathered} u=\frac{-21\pm\sqrt[]{9}}{-18} \\ \\ u=(-21\pm3)/(-18) \end{gathered}`

The values of u are

u=1 and u=4/3

Remember that

u=cosx

For u=1

the interval is [0,360) ----> the value of 360 degrees is not included

cosx=1 ------> the value of x=0 degrees

For u=4/3

cosx=4/3 -------> is not a solution (cosine cannot be greater than 1)

therefore

The solution is x=0 degrees