Question

The baseball diamond is really a square. The distance each other base is 90 feet. how far does the catcher have to throw the ball to get the home plate to second base? round your answer to the nearest foot

Answer 1

The Diagonal of a Square

To throw the ball from the home plate to the second base, the ball must travel a distance equal to the diagonal of the square of a side of 90 ft.

The diagonal of a square divides it into two identical right triangles, where the hypotenuse is the length of the diagonal and the two equal legs are the length of each side.

The length of the diagonal can be calculated by using the Pythagora's Theorem:

`d=a^2+a^2`

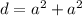
Where d is the length of the diagonal and a is the side length of the square. Operating:

`\begin{gathered} d^2=2a^2 \\ d=\sqrt[]{2}\text{ }a \end{gathered}`

Given the value of a = 90 ft:

`\begin{gathered} d=1.41\cdot90 \\ d\approx127ft \end{gathered}`

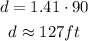
Answer: C. 127 feet