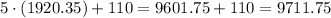We have two investments for Sherrie.
The first, an unknown amount X at 13% interest.
The second investment is a capital of $110 more than five times the amount X, invested 5 times within the year, at a rate of 8%.
The interest of the first investment, after one year (t=1), can be calcualted as:
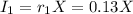
The interest for the second investment can be calculated as:
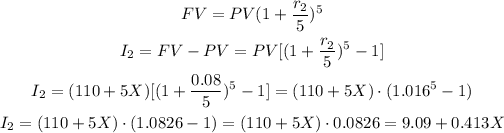
We know that the total interest in the year is $1051.84.
Then, the value X can be calculated as:
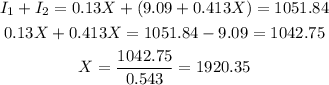
At 13% rate, Sherrie invested $1920.35.
At 8% rate, Sherrie invested $9711.75.