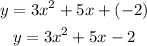Question

Find the equation of a parabola that passes through the points (1,6) (2,20) and (3,40)

Answer 1

∵ The form of the equation of the parabola is

`y=ax^2+bx+c`

∵ The points (1, 6), (2, 20), and (3, 40) lie on it

∴ x1 = 1 and y1 = 6, x2 = 2 and y2 = 20, x3 = 3 and y3 = 40

→ Substitute these values in the equation above to make 3 equations and solve

them together to find the values of a, b, and c

`\begin{gathered} 6=a(1)^2+b(1)+c \\ 6=a+b+c \end{gathered}`

∴ a + b + c = 6 ====== (1)

`\begin{gathered} 20=a(2)^2+b(2)+c \\ 20=4a+2b+c \end{gathered}`

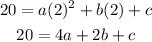
∴ 4a + 2b + c = 20 ===== (2)

`\begin{gathered} 40=a(3)^2+b(3)+c \\ 40=9a+3b+c \end{gathered}`

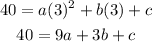
∴ 9a + 3b + c = 40 ===== (3)

Now we will solve the 3 equations to find a, b, and c

We can do that using the calculator or manual

By using the calculator

∴ a = 3, b = 5, and c = -2

Let us substitute them in the form of the equation above

`\begin{gathered} y=3x^2+5x+(-2) \\ y=3x^2+5x-2 \end{gathered}`