We have here an arithmetic progression.
We have that the common difference is:
53- 60 = - 7
46 - 53 = - 7
39 - 46 = - 7
And so on.
Therefore, the common difference of this sequence is d = -7. The progression is decreasing.
We can find the formula for the sequence using the general formula for arithmetic progressions:
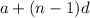
Where
a is the first term of the arithmetic progression.
n is the n term of the sequence.
d is the common difference ( d = -7 in this case).
Then, we have that the formula for this sequence is:
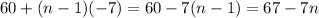
We can check that the second, and six terms are:
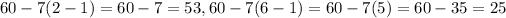
We have:
60 (1), 53 (2), 46 (3), 39 (4), 32 (5), 25 (6), ...
Therefore, the tenth term for this sequence is:
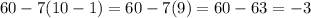
Hence, the tenth term is -3.