Solution:
Given:
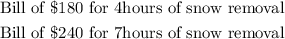
To get the fixed reservation rate and the charge per hour, we find the equation in the form of the equation of a line.
The equation of a line is of the form,
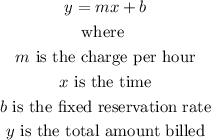
Hence, we develop the equations for both bills and then solve for the unknowns.
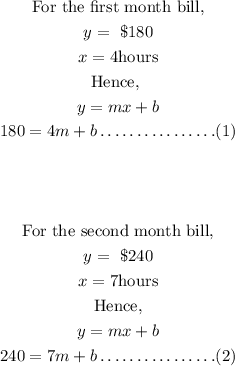
Solving equation (1) and (2) simultaneously by elimination method;

Since the constants are known, we can deduce that;
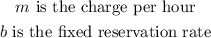
Therefore,
The fixed reservation rate is $100
The charge per hour is $20
The equation of the line that represents the company's fixed reservation rate and charge per hour will be;
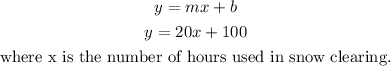
Hence, the equation is;
