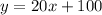Question

For two months, Martin used the same snow removal company to help clear his property. The company had a fixedreservation rate per month, plus an hourly rate for the amount of time that is spent clearing snow. Martin receivedtwo bills from the snow removal company. The first bill was $180 for 4 hours of snow removal and the second billwas $240 for 7 hours of snow removal. Find the equation of the line that represents the snow removal company'sfixed reservation rate and charge per hour. Round to the nearest cent if necessary.

Answer 1

Given:

`\begin{gathered} \text{Bill of \$180 for 4hours of snow removal} \\ \text{Bill of \$240 for 7hours of snow removal} \end{gathered}`

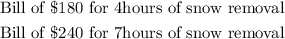
To get the fixed reservation rate and the charge per hour, we find the equation in the form of the equation of a line.

The equation of a line is of the form,

`\begin{gathered} y=mx+b \\ \text{where } \\ m\text{ is the charge per hour} \\ x\text{ is the time} \\ b\text{ is the fixed reservation rate} \\ y\text{ is the total amount billed} \end{gathered}`

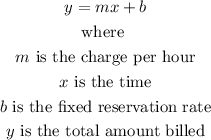
Hence, we develop the equations for both bills and then solve for the unknowns.

`\begin{gathered} \text{For the first month bill,} \\ y=\text{ \$180} \\ x=4\text{hours} \\ \text{Hence, } \\ y=mx+b \\ 180=4m+b\ldots\ldots\ldots\ldots\ldots.\mathrm{}(1) \\ \\ \\ \\ \text{For the second month bill,} \\ y=\text{ \$240} \\ x=7\text{hours} \\ \text{Hence,} \\ y=mx+b \\ 240=7m+b\ldots\ldots\ldots\ldots\ldots\text{.}\mathrm{}(2) \end{gathered}`

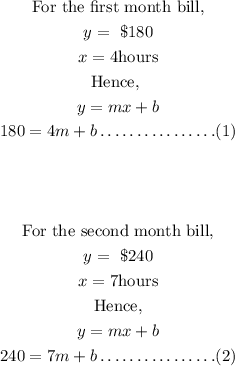
Solving equation (1) and (2) simultaneously by elimination method;

`\begin{gathered} 4m+b=180\ldots.\ldots\ldots.\ldots\ldots\text{.}(1) \\ 7m+b=240\ldots\ldots\ldots\ldots\ldots\ldots(2) \\ \\ \text{Subtracting equation (1) from (2),} \\ equation(2)-\text{equation}(1) \\ 7m-4m+b-b=240-180 \\ 3m=60 \\ \text{Dividing both sides by 3;} \\ m=(60)/(3) \\ m=20 \\ \\ \\ To\text{ get b, substitute m in equation (1),} \\ 4m+b=180 \\ 4(20)+b=180 \\ 80+b=180 \\ b=180-80 \\ b=100 \end{gathered}`

Since the constants are known, we can deduce that;

`\begin{gathered} m\text{ is the charge per hour} \\ b\text{ is the fixed reservation rate} \end{gathered}`

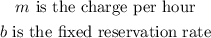
Therefore,

The fixed reservation rate is $100

The charge per hour is $20

The equation of the line that represents the company's fixed reservation rate and charge per hour will be;

`\begin{gathered} y=mx+b \\ y=20x+100 \\ \text{where x is the number of hours used in snow clearing.} \end{gathered}`

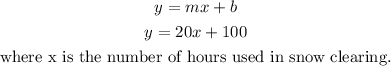
Hence, the equation is;

`y=20x+100`