Question

Find the perimeter of triangle ABC with vertices at (4,5), (10,5), and (4,-3). Round your answer to the nearest tenth (1 decimal place!)

Answer 1

We have the following equation to find the distance between two points A and B:

`d(A,B)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

In this case, if the points are A=(4,5), B=(10,5) and C=(4,-3), then we can find the length of the sides of the triangle using the formula for the distance between two points:

`\begin{gathered} A=(4,5) \\ B=(10,5) \\ C=(4,-3) \\ --------------------------- \\ d(A,B)=\sqrt[]{(10-4)^2+(5-5)^2}=\sqrt[]{(6)^2}=6 \\ d(A,C)=\sqrt[]{(4-4)^2+(-3-5)^2}=\sqrt[]{(-8)^2}=\sqrt[]{64}=8 \\ d(B,C)=\sqrt[]{(4-10)^2+(-3-5)^2}=\sqrt[]{(-6)^2+(-8)^2}=\sqrt[]{36+64} \\ =\sqrt[]{100}=10 \end{gathered}`

then, if we add the 3 distances, we can find the perimeter of the triangle:

`\begin{gathered} P=d(A,B)+d(A,C)+d(B,C)=6+8+10=24 \\ P=24 \end{gathered}`

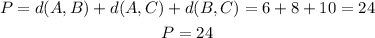
therefore, the perimeter of the triangle is 24 units