Question

Please help with calculusFind the derivative : cos^2 x

Answer 1

From the problem, we have :

`\cos ^2x`

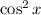
Note that it is the same as :

`\cos ^2x=(\cos x)^2`

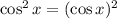
And using the general derivative formula :

`(d(u^n))/(dx)=nu^(n-1)du`

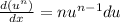
The exponent will be multiplied to u raised to n-1 and the derivative of u.

Going back to the problem :

`(d(\cos x)^2)/(dx)=2\cos x\cdot d(\cos x)`

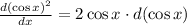
Note that the derivative of cos x is -sin x

`\begin{gathered} 2\cos x\cdot d(\cos x)=2\cos x(-\sin x) \\ \Rightarrow-2\cos x\sin x \end{gathered}`

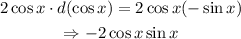
Take note also of the identity :

`\sin 2x=2\sin x\cos x`

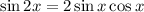
So the expression will be :

`-2\sin x\cos x=-\sin 2x`

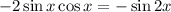
The answer is -sin 2x