From the problem, we have :
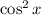
Note that it is the same as :
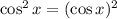
And using the general derivative formula :
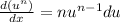
The exponent will be multiplied to u raised to n-1 and the derivative of u.
Going back to the problem :
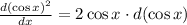
Note that the derivative of cos x is -sin x
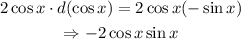
Take note also of the identity :
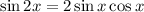
So the expression will be :
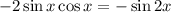
The answer is -sin 2x