Let t be how many he kept, r how many he gave to Ryan and n how many he gave to Neil.
The total have to still be 47, so:

If he gave Neil 3 less than Ryan, than the number he gave to Neil plus 3 will be the number he gave to Ryan, so:
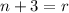
And if he kept 5 mre than Ryan, the number he kept is equal the number he gave Ryan plus 5:
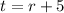
Since we want to know the number he kept, t, we can substitute the other variables so that we have an equation with only the variable t.
So, since r is in all equations, let's first solve the second for n and substitute it into the first, which will reduce the system to only 2 variables:
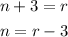
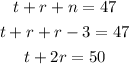
Now, we can solve the third equation for r and substitute it into the above one:
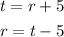
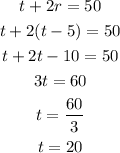
So, Tom kept 20 for himself.