Question

Livingston is a growing industrial town. Every year, the level of CO2 emissions from the town increases by 7%. If the town produced 318,280 metric tons of CO2 this year, how much will be produced 12 years in the future?If necessary, round your answer to the nearest whole number. metric tons

Answer 1

This situation can be modeled by the exponential growth equation, which is:

`f(t)=a(1+r)^t^{}`

where a is the initial amount, r is the growth rate (as a decimal), and t is time.

In this case, f(t) represents the level of CO2 emissions, the initial amount is 318,280 metric tons of CO2, and r is 0.07. Replacing these values, and t = 12, we get:

`\begin{gathered} f(12)=318,280\cdot(1+0.07)^(12) \\ f(12)=318,280\cdot2.252 \\ f(12)\approx716,828 \end{gathered}`

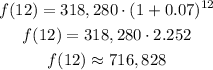
12 years in the future, 716,828 metric tons of CO2 will be produced