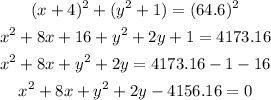Question

Earth is represented on a map of a portion of the solar system so that its surface is the circle with equation x2+y2+8x+2y−4079=0. A weather satellite circles 0.6 unit above Earth with the center of its circular orbit at the center of Earth. Find the general form of the equation for the orbit of the satellite on this map.

Answer 1

`x^2+8x+y^2+2y-4156.16=0`

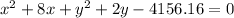
Explanation:

We have the following equation:

`x^2+y^2+8x+2y-4079=0`

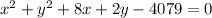
From this equation we must calculate the standard way to calculate the radius, it would look like this:

`\begin{gathered} x^2+8x+y^2+2y=4076 \\ x^2+8x+16+y^2+2y+1=4076+16+1 \\ (x+4)^2+(y^{}+1)^2=4096 \\ (x+4)^2+(y^{}+1)^2=64^2 \\ r=64 \end{gathered}`

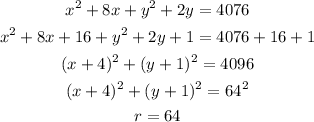
Now, we know that the radius is 64, but we are told that a weather satellite circles 0.6 unit above Earth with the center of its circular orbit at the center of Earth, so we must add 0.6 to the radius and then develop to calculate the equation of the satellite:

`\begin{gathered} (x+4)^2+(y^2+1)=(64.6)^2 \\ x^2+8x+16+y^2+2y+1=4173.16 \\ x^2+8x+y^2+2y=4173.16-1-16 \\ x^2+8x+y^2+2y-4156.16=0 \end{gathered}`