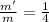Given
The spring constant of a simple harmonic oscillator is quartered
To find
By what factor will the mass of the system need to change in order for the frequency of the motion to remain the same?
Step-by-step explanation
The frequency of the harmonic oscillator is given by
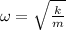
where k is the spring constant and m is the mass
A/q,
The spring constant is quatered and the frequency remains same.
After the change let the mass be m'
Thus,
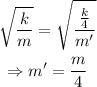
Conclusion
The mass should also be quatered so that the fequency is same