Question

An endangered species of fish has a population that is decreasing exponentially (A = A0 * e^kt). The population 9 years ago was 1500. Today, only1000 of the fish are alive. Once the population drops below 100, the situation will be irreversible. When will this happen, according to themodel? (Round to the nearest whole year.)

Answer 1

In order to calculate when the population will be 100, first let's calculate the coefficients A0 and k.

Since the initial population is 1500, we have A0 = 1500.

Then, to calculate the coefficient k, let's use the value of t = 9 and A = 1000, so we have:

`\begin{gathered} 1000=1500\cdot e^(k\cdot9) \\ e^(9k)=(1000)/(1500)=(2)/(3) \\ \ln (e^(9k))=\ln ((2)/(3)) \\ 9k\cdot\ln (e)=-0.405465 \\ 9k=-0.405465 \\ k=-0.045 \end{gathered}`

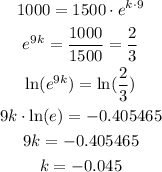
Now, let's calculate the value of t for A = 100:

`\begin{gathered} 100=1500\cdot e^(-0.045\cdot t) \\ e^(-0.045t)=(100)/(1500)=(1)/(15) \\ \ln (e^(-0.045t))=\ln ((1)/(15)) \\ -0.045t\cdot\ln (e)=-2.70805 \\ -0.045t=-2.70805 \\ t=(-2.70805)/(-0.045)=60.18 \end{gathered}`

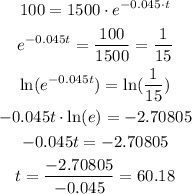
Rounding to the nearest whole year, we have a time of 60 years.