In order to calculate when the population will be 100, first let's calculate the coefficients A0 and k.
Since the initial population is 1500, we have A0 = 1500.
Then, to calculate the coefficient k, let's use the value of t = 9 and A = 1000, so we have:

Now, let's calculate the value of t for A = 100:
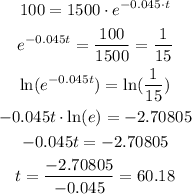
Rounding to the nearest whole year, we have a time of 60 years.