Question

Two cards are selected from a standard deck of 52 playing cards. The first is replaced before the second card is selected. Find the probability of selecting a spade and then selecting of ten.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Define the formula for probability

`\text{Probability}=\frac{\text{number of required outcome }}{\text{number of total outcome}}`

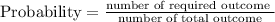
STEP 2: Get the required number of cards

`\begin{gathered} A\text{ standard deck of playing cards has 52 cards therefore,} \\ \text{ number of total outcomes=52} \\ A\text{ standard deck of playing cards has }13\text{ spades} \\ A\text{ standard deck of playing cards has }4\text{ tens} \end{gathered}`

STEP 3: Calculate the probability for getting a spade

`\begin{gathered} \text{Pr(spades)}=\frac{\text{number of spades }}{\text{number of total outcome}} \\ \text{Pr(spades)}=(13)/(52)=(1)/(4) \end{gathered}`

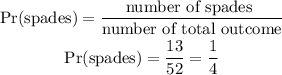
STEP 4: Calculate the probability for getting a ten

Since the cards were replaced, the number total outcomes remains the same

`\begin{gathered} \text{Pr(ten)}=\frac{\text{number of ten}}{\text{number of total outcome}} \\ \text{Pr(ten)}=(4)/(52)=(1)/(13) \end{gathered}`

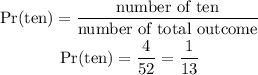
STEP 5: Calculate the probability of selecting a spade and then selecting a ten

`\begin{gathered} \text{The probability of selecting a spade and then a ten is;} \\ Pr(\text{spade)}* Pr(ten) \\ =(1)/(4)*(1)/(13)=(1)/(52) \end{gathered}`

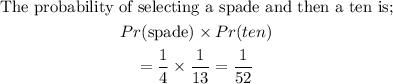
Hence, the probability of selecting a spade and then selecting a ten is 1/52