Question

Would someone walk me through this? I recognize it but can’t remember how to begin.

Answer 1

The given inequality is 2x-3y < 5.

To find the ordered pairs that satisfy the inequality, we have to evaluate it.

For (2,0).

`\begin{gathered} 2(2)-3(0)<5 \\ 4-0<5 \\ 4<5 \end{gathered}`

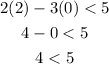
Given that 4<5 is true, we can conclude that (2,0) satisfies the inequality.

For (1,-1).

`\begin{gathered} 2(1)-3(-1)<5 \\ 2+3<5 \\ 5<5 \end{gathered}`

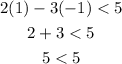
The statement 5<5 is false. So, (1,-1) does not satisfy the inequality.

For (0,0).

`\begin{gathered} 2(0)-3(0)<5 \\ 0<5 \end{gathered}`

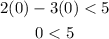
The statement 0<5 is true. So, (0,0) is a solution to the given inequality.

For (2,4).

`\begin{gathered} 2(2)-3(4)<5 \\ 4-12<5 \\ -8<5 \end{gathered}`

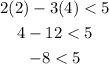
Given that -8<5 is correct. (2,4) satisfies the inequality.

Therefore, the solutions are (2,0), (0,0), and (2,4).