Question

What is the 10th term of the geometric sequence where a1 = 8,192 and a3 = 512? (1 point)0.031250.06250.1250.15625

Answer 1

I just did it and 0.03125 is correct

Explanation:

Answer 2

Hello!

Let's write some important information that we know:

• a1 ,= 8,192

,

• a3 ,= 512

,

• q ,= ?

First, we have to discover the value of q, using the formula below:

`a_n=a_1\cdot q^(n-1)`

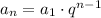
Let's replace n as 3:

`\begin{gathered} 512=8,192\cdot q^(3-1) \\ 512=8,192\cdot q^2 \\ 8,192q^2=512 \\ q^2=(512)/(8192)=(1)/(16) \\ \\ q^=\sqrt{(1)/(16)}=(√(1))/(√(16))=(1)/(4) \\ \end{gathered}`

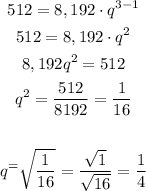
So, q = 1/4.

With this information, now we are able to calculate the 10th term, using the same formula:

`\begin{gathered} a_n=a_1\cdot q^(n-1) \\ a_(10)=8,192\cdot((1)/(4))^(10-1) \\ \\ a_(10)=8,192\cdot((1)/(4))^9 \\ \\ \boxed{\mathrm{a_(10)=(1)/(32)}=0.03125} \end{gathered}`

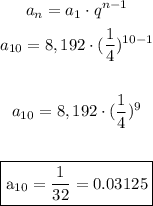
Answer:

Alternative A. 0.03125