Hello!
Let's write some important information that we know:
• a1 ,= 8,192
,
• a3 ,= 512
,
• q ,= ?
First, we have to discover the value of q, using the formula below:
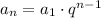
Let's replace n as 3:
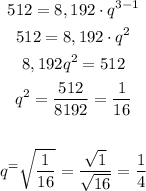
So, q = 1/4.
With this information, now we are able to calculate the 10th term, using the same formula:
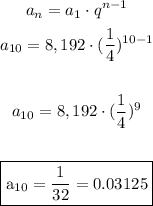
Answer:
Alternative A. 0.03125