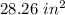Answer:
The approximate area of the smaller circle is;
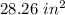
Step-by-step explanation:
Given that the radius of a smaller circle is half the length of the radius of a larger circle.
Let R and r represent the radius of the larger and smaller circle respectively;

The area of the smaller circle will be;

while the area of the larger circle will be;
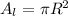
substituting R = 2r;

We can now replace the area of the smaller circle;
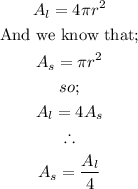
Given in the question;
The area of the larger circle is 113.04 square inches.
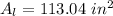
Substituting the area of the larger circle;
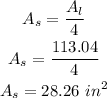
Therefore, the approximate area of the smaller circle is;