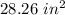Question

14. The radius of a smaller circle is half the length of the radius of a larger circle.The area of the larger circle is 113.04 square inches. What is the approximate areaof the smaller circle?

Answer 1

The approximate area of the smaller circle is;

`28.26\text{ }in^2`

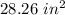
Step-by-step explanation:

Given that the radius of a smaller circle is half the length of the radius of a larger circle.

Let R and r represent the radius of the larger and smaller circle respectively;

`R=2r`

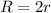
The area of the smaller circle will be;

`A_s=\pi r^2`

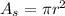
while the area of the larger circle will be;

`A_l=\pi R^2`

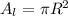
substituting R = 2r;

`\begin{gathered} A_l=\pi R^2 \\ A_l=\pi(2r)^2 \\ A_l=\pi(2^2r^2) \\ A_l=4\pi r^2 \end{gathered}`

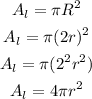
We can now replace the area of the smaller circle;

`\begin{gathered} A_l=4\pi r^2 \\ \text{And we know that;} \\ A_s=\pi r^2 \\ so; \\ A_l=4A_s \\ \therefore \\ A_s=(A_l)/(4) \end{gathered}`

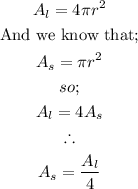
Given in the question;

The area of the larger circle is 113.04 square inches.

`A_l=113.04\text{ }in^2`

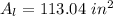
Substituting the area of the larger circle;

`\begin{gathered} A_s=(A_l)/(4) \\ A_s=(113.04)/(4) \\ A_s=28.26\text{ }in^2 \end{gathered}`

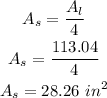
Therefore, the approximate area of the smaller circle is;

`28.26\text{ }in^2`