Solution
We are given the function
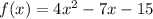
To find the x - intercept, we will put f(x) = 0
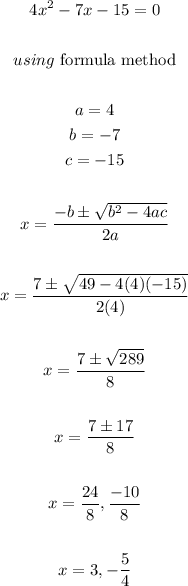
The x - intercept are
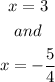
f(x) vertex is a minimum
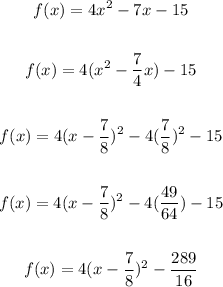
The coordinate of the vertex is
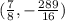
The graph of the function is
Basically, we use the vertex point, intercept on the x - axis and y - axis