We have the system of equations:
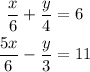
We can solve it by elimination: we will multiply the first equation by 5 and substract from the second equation. Then, we will eliminate x and we can solve for y.
We can write this as:
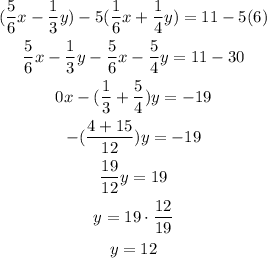
Now, with the value of y, we can solve for x as:
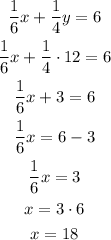
Answer: x=18 and y=12