EJERCICIO DE ESTADISTICAThe time (in minutes) between telephone calls at an insurance claims office has the exponential probability distributionf(x) = 0.50 e-0.50x for x ≥ 0.a. …

Question

asked Feb 16, 2023 41.3k views

1 Answer

Singuliere · Answer 1 · 2023-02-19T21:34:36+0000

Given

Exponential probability distribution

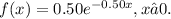
$f\mleft(x\mright)=0.50e^(-0.50x),x≥0.$

Find

a) what is the mean time between phone calls?

b) what is probability of 30 seconds or less between phone calls?

c) what is probability of 1 minute or less between phone calls?

d) what is probability of 5 or more minutes without a phone call?

Step-by-step explanation

given

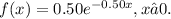
$f\mleft(x\mright)=0.50e^(-0.50x),x≥0.$

formula for the probability exponential distribution is given by

$\begin{gathered} P(x\leq a)=1-e^{-(a)/(\mu)} \\ P(aa) the mean is the reciprocal of the constant , so[tex]\mu=(1)/(0.50)=2$

b) probability of 30 seconds or less between phone calls is

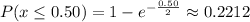
$P(x\leq0.50)=1-e^{-(0.50)/(2)}\approx0.2212$

c) probability of 1 minute or less between phone calls

$P(x\leq1)=1-e^{-(1)/(2)}\approx0.3935$

d)

probability of 5 or more minutes without a phone call

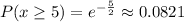
$P(x\ge5)=e^{-(5)/(2)}\approx0.0821$

Final Answer

Therefore ,

a) 2 minutes

b) 0.2212

c) 0.3935

d) 0.0821