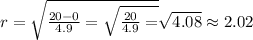Question

109. Effect of Gravity on Earth If a rock falls from a height of 20 meters on Earth, the height H (in meters) after r seconds is approximately H(x) = 20 - 4.9r? (a) What is the height of the rock when x = 1 second? When r = 1.1 seconqds? When x = 1.2 seconds? (b) When is the height of the rock 15 meters? When is it 10 meters? When is it 5 meters? (c) When does the rock strike the ground?

Answer 1

We have the expression for the height H of the rock in function of the time r, when it falls from a height of 20 meters:

`H(r)=20-4.9\cdot r^2`

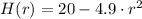
When r = 1 second, we have:

`H(1)=20-4.9(1)^2=20-4.9\cdot1=20-4.9=15.1`

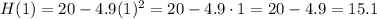
When r = 1.1 seconds, we have:

`H(1.1)=20-4.9(1.1)^2=20-4.9\cdot1.21=20-5.929=14.071\approx14`

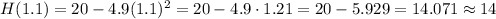
When r = 1.2 seconds, we have:

`H(1.2)=20-4.9(1.2)^2=20-4.9\cdot1.44=20-7.056=12.944\approx13`

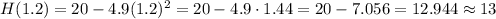
To know the time for each height, we have to work with the equation like this:

`\begin{gathered} H=20-4.9r^2 \\ 4.9r^2=20-H \\ r^2=(20-H)/(4.9) \\ r=\sqrt{(20-H)/(4.9)} \end{gathered}`

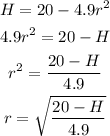
Then, we can calculate at which time the height is 15 meters:

`r=\sqrt{(20-15)/(4.9)=\sqrt{(5)/(4.9)}}=√(1.02)\approx1.01`

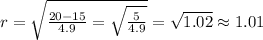
When the height is 10 meters, r is:

`r=\sqrt{(20-10)/(4.9)=\sqrt{(10)/(4.9)=}}√(2.04)\approx1.43`

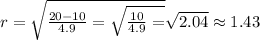
When the height is 5 meters, r is:

`r=\sqrt{(20-5)/(4.9)=\sqrt{(15)/(4.9)=}}√(3.06)\approx1.75`

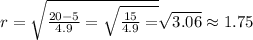
The rock hits the ground when H=0. This happens when r is:

`r=\sqrt{(20-0)/(4.9)=\sqrt{(20)/(4.9)=}}√(4.08)\approx2.02`