The perimeter is the whole sides of the figure. The figure has a rectantangle and an attached semi circle.
The circumfernce of a circle is the perimeter of a circle. The circumference of a circle is
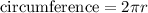
Since the attached part is a semi circle the circumference will be
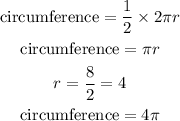
perimeter of the figure is therefore,
