Question

Solve the triangle. Round your answers to the nearest tenth.A. m∠B=118, a=16, c=18B. m∠B=118, a=14, c=18C. m∠B=118, a=18, c=18D. m∠B=118, a=17, c=18

Answer 1

General category: Mathematics.

Sub-category: Triangles.

Topic: Law of Sines

Introduction:

The Law of Sines is the relationship between the sides and angles of oblique triangles. This law states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all sides and angles in a given triangle.

Step-by-step explanation:

In a triangle ABC, the Law of Sines tell us the following expression:

`(a)/(\sin(A))=(b)/(\sin(B))=(c)/(\sin(C))`

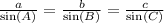
Consider the following oblique triangle:

Here:

CB= a

CA= b

AB= c

∠B= 180 - (32 +30)= 180 - 62 = 118

Now, applying the law of sines, we get the following expression:

`(CB)/(\sin(30\degree))=(30)/(\sin(118\degree))=(AB)/(\sin(32\degree))`

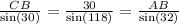
Then, we get the following equations:

Equation 1:

`(CB)/(\sin(30\degree))=(30)/(\sin(118\degree))`

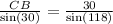
Equation 2:

`(30)/(\sin(118\degree))=(AB)/(\sin(32\degree))`

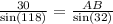
From equation 1, we obtain:

`a=CB=\frac{30\cdot\text{ }\sin(30\degree)}{\sin(118\degree)}=\text{ 16.98855}\approx17`

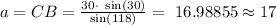
From equation 2, we get:

`c=AB=\frac{30\cdot\text{ }\sin(32\degree)}{\sin(118\degree)}=18.00512\approx18`

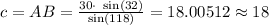
We can conclude that the correct answer is:

Answer:

m∠B=118

a= 17

c= 18