General category: Mathematics.
Sub-category: Triangles.
Topic: Law of Sines
Introduction:
The Law of Sines is the relationship between the sides and angles of oblique triangles. This law states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all sides and angles in a given triangle.
Step-by-step explanation:
In a triangle ABC, the Law of Sines tell us the following expression:
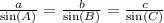
Consider the following oblique triangle:
Here:
CB= a
CA= b
AB= c
∠B= 180 - (32 +30)= 180 - 62 = 118
Now, applying the law of sines, we get the following expression:
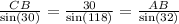
Then, we get the following equations:
Equation 1:
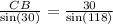
Equation 2:
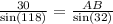
From equation 1, we obtain:
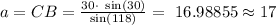
From equation 2, we get:
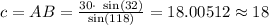
We can conclude that the correct answer is:
Answer:
m∠B=118
a= 17
c= 18