Question

here are some transformation rules. For each rule, describe whether the transformation is a rigid motion, a dilation, or neither.

Answer 1

Step-by-step explanation

In a rigid motion a figure is translated but its shape and size remains equal whereas in a dilation the size of the figure changes but its shape is conserved. Rigid motion transformations imply adding or substracting constant to the coordinates of the points belonging to a figure whereas in a dilation the x and y values are multiplied by the same number. This preserves the sahpe, if they are multiply by different numbers then it's no longer a dilation.

So let's analyze each transformation. The first one is:

`(x,y)\rightarrow(x-2,y-3)`

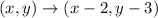
As you can see you only substract constant from the original coordinates of each point which means that this transformation is a rigid motion.

The second transformation is:

`(x,y)\rightarrow(2x,3y)`

Here both coordinates are multiplied by different numbers which means that this is neither a dilation or a rigid motion.

The third one is:

`(x,y)\rightarrow(3x,3y)`

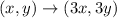
Both coordinates are multiplied by the same number which implies that this transformation is a dilation.

Finally the fourth one is:

`(x,y)\rightarrow(2-x,y)`

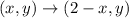
Here the first coordinate is multiplied by -1 and the second remains the same so this is neither a dilation or a rigid motion.

Answers

a. Rigid Motion

b. Neither

c. Dilation

d. Neither