Question

Use Descartes Rule of Signs to complete the chart with the possibilities for the nature of the roots of the equations:A) 2x^5 - x^3 - 4x^2 + x - 2 =0B) 2x^4 - 9x^3 + 13x^2 - x -5 =0

Answer 1

In these two problems, we will apply the Descartes Rule of Signs:

- the number of positive real zeros in a polynomial function f(x) is the same or less than by an even numbers as the number of changes in the sign of the coefficients.

Let's begin with the first polynomial from Part A):

`2x^5-x^3-4x^2+x-2=0`

In the original expression, we see three sign changes:

`2x^5(here)-x^3-4x^2(here)+x(here)-2`

Since there are three changes, we will have have the possibility oft3positive real roots. or 1 positive real root

Nex, we evaluate the expression with -x and check for changes:

`\begin{gathered} 2(-x)^5-(-x)^3-4(-x)^2+(-x)-2=0 \\ -2x^5+x^3-4x^2-x-2=0 \end{gathered}`

This time, we have two changes to the signs:

`-2x^5(here)+x^3(here)-4x^2-x-2=0`

Therefore we have 2 or 0 possible negative roots.

Finally, we need to determine how many imaginary conjugates are possible.

We will need to use the combinations of possible positive and negative roots to do this. It's will get a bit complicated, so we'll make a chart.

Now, let's look at Part B).

This time we have the equation

`2x^4-9x^3+13x^2-x-5=0`

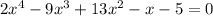
Let's check for positive roots by checking sign changes. It looks like we have three sign changes:

`2x^4(here)-9x^3(here)+13x^2(here)-x-5=0`

That means we have 3 or 1 positive roots.

Evaluate -x to check for negative roots:

`\begin{gathered} 2(-x)^4-9(-x)^3+13(-x)^2-(-x)-5 \\ 2x^4+9x^3+13x^2+x-5 \end{gathered}`

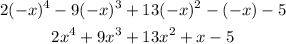
We have only one sign change this time:

`2x^4+9x^3+13x^2+x(here)-5`

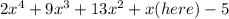
There is only one possible negative root.

Now we need to test for imaginary roots. Similar to the last problem, we will use a chart.