To answer the question, follow the steps below.
Step 01: Find the speed upstream.
The speed is the ratio between the distance (miles) and the time (hours).
So, the speed upstream (su) is:
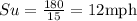
Step 02: Find the speed downstream.
sd is:
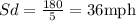
Step 03: Write an equation for each speed.
Consider:
a = speed of tugboat
b = speed of current
Then,

Step 04: Isolate "a" in the first equation.
To do it, add "b" to both sides.
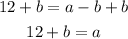
Step 05: Substitute a by 12 + b in the second equation.
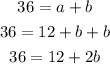
To isolate b, subtract 12 from both sides, then divide the sides by 2.
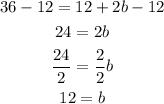
Step 06: Substitute b by 12 in the equation from step 04.
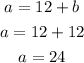
Answer:
The speed of the tugboat is 24 mpf.
The speed of the current is 12 mpf.