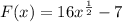Question

Find the particular antiderivative F(x) of f(x)=8/sqreroot xthat satisfies F(1) = 9.

Answer 1

Given:

`f(x)=\frac{8}{\sqrt[]{x}}`

The above can be re-written as;

`f(x)=\frac{8}{x^{(1)/(2)}}=8x^{-(1)/(2)}`
`f(x)=8x^{-(1)/(2)}`

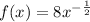
Applying the rule of antiderivatives of basic function;

`x^ndx=(x^(n+1))/(n+1)`

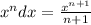
Then we have;

`F(x)=\frac{8x^{-(1)/(2)+1}}{-(1)/(2)+1}`
`F(x)=\frac{8x^{(1)/(2)}}{(1)/(2)}`
`=8x^{(1)/(2)}*2`
`=16x^{(1)/(2)}+C`

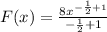
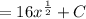
Hence;

`F(x)=16x^{(1)/(2)}+C`

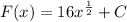
But from the question; F(1) = 9

Substitute x =1 into F(x) and equate to 9 to find C.

That is;

`F(1)=16(1)^{(1)/(2)}+C=9`

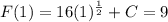
⇒ 16 + C = 9

Subtract 16 from both-side of the equation.

C = 9 - 16

C = -7

Substitute the value of C back into the anti derivative F(x).

Therefore,

The antiderivative that satisfies F(x) of the function that satisfies F(1) = 9 is:

`F(x)=16x^{(1)/(2)}-7`