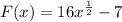Given:
![f(x)=\frac{8}{\sqrt[]{x}}](https://img.qammunity.org/2023/formulas/mathematics/college/c6f2m6lur0al83sidgbq07r4212p3tgode.png)
The above can be re-written as;
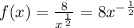
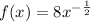
Applying the rule of antiderivatives of basic function;
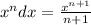
Then we have;
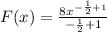
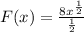
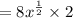
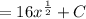
Hence;
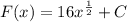
But from the question; F(1) = 9
Substitute x =1 into F(x) and equate to 9 to find C.
That is;
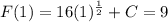
⇒ 16 + C = 9
Subtract 16 from both-side of the equation.
C = 9 - 16
C = -7
Substitute the value of C back into the anti derivative F(x).
Therefore,
The antiderivative that satisfies F(x) of the function that satisfies F(1) = 9 is: