We have the following complex number:
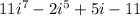
Let's begin by noting how the powers of i work. To begin with, let's remember that
![i=\sqrt[]{-1}\text{.}](https://img.qammunity.org/2023/formulas/mathematics/high-school/vlyux1x6tfbgzxkpruehyi1e6sq68x3u68.png)
Knowing that:
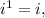
![i^2=(\sqrt[]{-1})^2=-1,](https://img.qammunity.org/2023/formulas/mathematics/high-school/sglot3g2ors6xxjd64zmksmhr2be91goej.png)
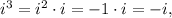
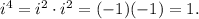
Now, notice that
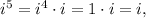
so the powers of i actually repeat after four integers. In other words:
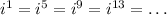
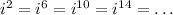
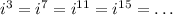
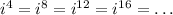
This also works the same way for negative powers. Now that we know this, let's focus on the powers of i on the number we were given:
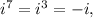
so
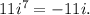
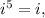
so
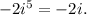
Putting all of them together:
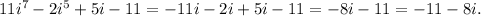
So, the correct answer is option c.