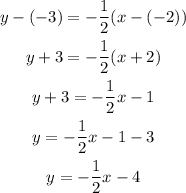Question

Write the slope-intercept form of the equation of the line described. 4 5) through: (-2, -3), perp. to y = 2x + 2 4) through: (3, -1), parallel to y = -x - 2 3 A) y 1 4 1 Х 2 - - 4 B) y=-5x + 3 5 1 B) y=-* 2 2. 1 5 -xt 2 2 4 A) y=-x-5 3 3 C) y = -x +5 4 1 C) y = -2x D) y= 2 4 D) y = 5x + 3

Answer 1

Use the given information to write the slope intercept form equation of each line:

We know one of the points the line passes through (-2,-3) and that the line is perpendicular to y=2x+2 it means the product between both slopes is -1

`\begin{gathered} m1\cdot m2=-1 \\ 2\cdot m2=-1 \\ m2=-(1)/(2) \end{gathered}`

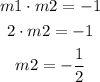
With this information, it is possible to write the equation of the line in slope point form and then find the slope intercept form

`\begin{gathered} y-(-3)=-(1)/(2)(x-(-2)) \\ y+3=-(1)/(2)(x+2) \\ y+3=-(1)/(2)x-1 \\ y=-(1)/(2)x-1-3 \\ y=-(1)/(2)x-4 \end{gathered}`