We are tasked to write an algebraic equation with distributive property and solve it using the two-column proof.
For an algebraic equation, I will use the equation
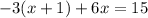
Let's start solving this problem by applying the distributive property on the first term -3(x+1). We have
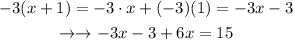
The next step is to add like terms. We add -3x and 6x on the left-hand side of the equation. We get
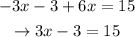
This will be followed by the addition property of equality. We add +3 on both sides of the equation so the -3 on the left-hand side of the equation will cancel out. We have
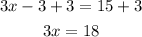
Finally, to solve the equation, we use the division property of equality. We divide both sides by 3. We get
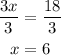
The steps are summarized as follows