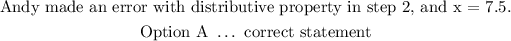Question

andy incorrectly solved an equation and showed his work.step 1: 5 (2r + 5) = 100Step 2: 10x + 5 = 100Step 3: 10x = 95Step 4: x = 9.5What error did Andy make, and what is the correct solution to his problem?a: Andy made an error with the distributive property in step 2, x = 7.5b: Andy made an error with the distributive property in step 2, x= 12.5c: Andy made an error with the associative property in step 2, x= 7.5d: Andy made an error with the subtraction property in step 2, x= 12.5

Answer 1

We will investigate the laws associated with algebraic manipulations of numbers.

There are a total of three Laws asscoiated with the algebraic operators as follows:

`\text{Commutative, Associative,Distributive}`

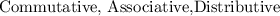
Commutative Law:

This law pertains to the order in which a addition " + " and multiplication " x " operators are applied on two numbers.

Lets say we have two numbers named ( a ) and ( b ). The commutative law representing additon would be:

`a\text{ + b = b + a}`

The multiplication operator would be:

`a\text{ x b = b x a }`

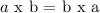
We see that exchange of numbers does not change the result of both addition and multiplication.

Associative Law:

This law pertains to the application of an addition " + " and multiplication " x " operators in groups. The grouping of numbers is represented by a parenthesis " ( ) ".

Lets say we have three numbers ( a , b and c ). We can have three possible combinations of grouping with each operator as follows:

Addition:

`a\text{ + ( b + c ) = b + ( a + c ) = c + ( a + b ) }`

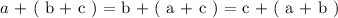
Multiplication:

`a\text{ x ( b x c ) = b x ( a x c ) = c x ( a x b )}`

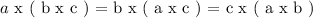
We see that each group of combination above for both addition and multiplication leads to the same result disregarding which pair is operated first!

Distributive Law:

This law pertains to an application of addition operator on two element group which is multiplied by a third number.

Using the same three numbers ( a,b, and c ) we have:

`c\text{ x ( a + b ) = }c\text{ x a + c x b}`

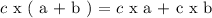
The above represents the solving of parenthesis by removing the round brackets " ( ) " and applying the multiplication operator with each element in the group.

Andy tries to solve an equation as follows:

`\text{Step 1: 5 }\cdot\text{( 2x + 5 ) = 100}`

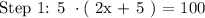
To remove the parenthesis on the left hand side of the " = " sign we need to apply the distributive law.

The next step involves the application of distributive law as follows:

`\begin{gathered} 5\cdot2x\text{ + 5}\cdot5\text{ = 100} \\ \text{Step 2: 10x + 25 = 100} \end{gathered}`

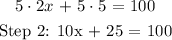
Therefore, we see that Andy applied the distributive law incorrectly in step 2. Where he applied the multiplication operator with just the first element of the group i.e ( 2x ) and left out on the second one i.e ( 5 ).

We will continue forward with the next step after applying the distributive law correctly. We will try to isolate the term involving the variable ( x ) by subtracting 25 on both sides of the " = " sign as follows:

`\begin{gathered} 10x\text{ + 25 - 25 = 100 - 25 } \\ \text{Step 3: 10x = 75} \end{gathered}`

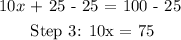
Then we will divide the entire equation by the multiple of the variable ( x ) as follows:

`\begin{gathered} (10x)/(10)\text{ = }(75)/(10) \\ \\ \text{Step4: x = 7.5} \end{gathered}`

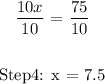
Therefore, the correction statement to Andy's solution would be:

`\begin{gathered} \text{Andy made an error with distributive property in step 2, and x = 7.5.} \\ \text{Option A }\ldots\text{ correct statement} \end{gathered}`