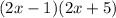SOLUTION
The given expression is
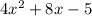
The general trinomial expression is,
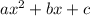
Therefore,
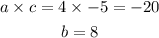
Let us look for the factors of -20 and also confirm if the factors will give 8 as the sum.
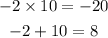
Therefore, the two factors are -2 and 10.
Let us now replace 8x with -2x and 10x in the expression given
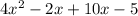
Break the expression into two groups
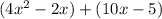
Factor out the common terms
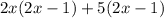
Factor out the common term 2x - 1
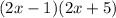
Hence, the answer is