Given:
Velocity of eagle = 28 m/s
Frequency of eagle = 370 Hz
Velocity of black bird = 11.35 m/s
Speed of sound = 343 m/s
Let's find the frequency the black bird hears as the eagle approaches the black bird.
Apply the formula;
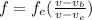
Where:
fe is frequency of eagle = 370 Hz
v = 343 m/s
vb is the frequency of the blackbird= 11.35 m/s
v = 343 m/s
ve is the speed of eagle = 28 m/s
Substitute values into the formula and solve for f:
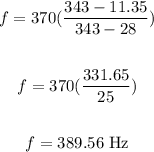
Therefore, the frequency the blackbird hear as the eagle appoaches is 389.56 Hz.
(b). Given:
Speed of eagle = 11.46.
What frequency does the blackbird hear (in Hz) after the eagle passes the blackbird?
Apply the formula:
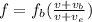
Where:
ve = 11.46 m/s
Thus, we have:

The frequency after the eagle passes the blackbird at this new speed is 370.12 Hz.
ANSWER:
• (a). 389.56 Hz.
• (b). 370.12 Hz.