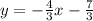Step-by-step explanation
Since we need a line that passes through the points (2,-5) and perpendicular to the line that passes through the points (x_1,y_1) = (−3, −2) and (x_2,y_2) = (5, 4).
We first need to compute the slope of this line by applying the slope formula:
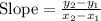
Substituting terms:
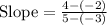
Subtracting numbers:
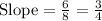
As the first line is perpendicular to the second, the slope should be negative and reciprocal.
Thus, the slope of the first line is slope= -4/3
Now, we already know that the equation of a line is as follows:
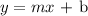
Where x=2 and y=-5 (the given point) and m=slope= -4/3
Plugging in the values into the equation:
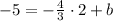
Multiplying numbers:
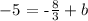
Adding +8/3 to both sides:
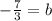
Finally, the equation of the line is the following: