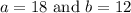To find:
Find the value of and so that () is everywhere differentiable.
Solution:
The limits of f(x) at x = -1 are:
![\lim_(x\to-1^-)f(x)=\operatorname{\lim}_(x\to-1^-)(ax^2+bx+4)=a-b+4...(1)]()
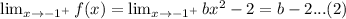
if a function is to be everywhere differentiable, then it must also be continuous everywhere. This implies that the one-sided limits must be equal.
Thus,
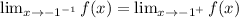
So, eq 1 = eq 2.
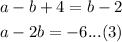
Next, the derivative one-sided limits must also equal at x = -1.
That is,
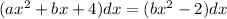
Thus,
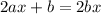
Substitute x = -1 in eq 4, then
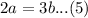
Solve eq 3 and eq 5 for a and b.