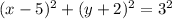Question

Write the standard form of the equation of the circle with the graph shown to the right.What is the standard form of the equation of the circle to the right?(Simplify your answer.)

Answer 1

From the image, we are shown a circle drawn on a graph and asked to find the standard form of the equation of the circle.

The standard form of the equation of a circle is denoted by the formula below.

`(x-a)^2+(y-b)^2=r^2`

Where c(a,b) represents the centre of the circle and r represents the radius of the circle.

From the equation above we would need the centre of the circle and the radius to find the equation of the circle.

Looking at the image if we pick out the coordinates of the centre indicated by the blue points and also trace the radius, we would have:

From the image, we can imply the following

`\begin{gathered} r=\text{radius}=3 \\ a=5 \\ b=-2 \end{gathered}`

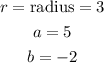
We will substitute the above values into the standard form for the equation of a circle

`\begin{gathered} (x-5)^2+(y-(-2))^2=3^2 \\ (x-5)^2+(y+2)^2=3^2 \end{gathered}`

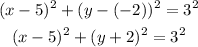
ANSWER: Therefore the standard form of the equation of the circle is

`(x-5)^2+(y+2)^2=3^2`