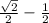Given the expression:
sin(135° - 60°)
Let's find the exact value of the expression.
First simplify the expression in the parentheses:
sin(135° - 60°) = sin(75°)
The exact value of sin(75°) is:
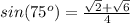
Part B.
Given the expression:
sin135° - cos60°
Let's find the exact value.
Apply the reference by finding the equivalent angle in the first quadrant.
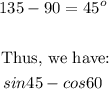
We have the following:
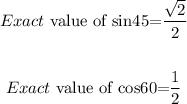
Therefore, the exact value of the expression is:
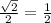
ANSWER:
• Part A.
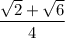
• Part B.