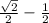Question

Find the exact value of each expression. (Only part B)

Answer 1

Given the expression:

sin(135° - 60°)

Let's find the exact value of the expression.

First simplify the expression in the parentheses:

sin(135° - 60°) = sin(75°)

The exact value of sin(75°) is:

`sin(75^o)=(√(2)+√(6))/(4)`

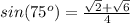
Part B.

Given the expression:

sin135° - cos60°

Let's find the exact value.

Apply the reference by finding the equivalent angle in the first quadrant.

`\begin{gathered} 135-90=45^o \\ \\ \text{ Thus, we have:} \\ sin45-cos60 \end{gathered}`

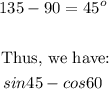
We have the following:

`\begin{gathered} Exact\text{ value of sin45=}(√(2))/(2) \\ \\ Exact\text{ value of cos60=}(1)/(2) \end{gathered}`

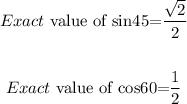
Therefore, the exact value of the expression is:

`(√(2))/(2)=(1)/(2)`

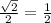
ANSWER:

• Part A.

`\begin{gathered} (√(2)+√(6))/(4) \\ \end{gathered}`

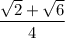
• Part B.

`(√(2))/(2)-(1)/(2)`