First, we have to calculate the measures of the sides of the triangle.
Apply the distance formula:
![d=\sqrt[]{(x2-x1)^2+(y2-y1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/1h551ypq5weta3sw0dynfch7nxiwrgmnba.png)
Replace with the coordinate points given:
A= (2,-8)
B= (5,-9)
C= (4,-6)
Side AC
![d=\sqrt[]{(4-2)^2+(-6-(-8))^2}=\sqrt[]{2^2+2^2}=\sqrt[]{8}](https://img.qammunity.org/2023/formulas/mathematics/college/3hl7sxs46qom4f7s2v5odt9sigsh883i4b.png)
Side CB
![d=\sqrt[]{(5-4)^2+(-9-(-6))^2}=\sqrt[]{1+9}=\sqrt[]{10}](https://img.qammunity.org/2023/formulas/mathematics/college/vhkqjdsubrmtbgt75lo1iy5qiyqeavjhtc.png)
Side AB
![d=\sqrt[]{(5-2)^2+(-9-(-8))}=\sqrt[]{9-1}=\sqrt[]{10}](https://img.qammunity.org/2023/formulas/mathematics/college/ym1jzl68y9nkfw8yr3hegl0muk4ewtpwoa.png)
Apply Heron's formula:
![A\text{ =}\sqrt[]{s(s-a)(s-b)(s-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/qk8hqvdi1ok4eavpo9wi1f585mm2sf31t8.png)
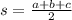
a, b, c are the distances ,CB , AC and AB
![s=\frac{\sqrt[]{10}+\sqrt[]{10}+\sqrt[]{8}}{2}=\frac{2\sqrt[]{10}+\sqrt[]{8}}{2}=4.58](https://img.qammunity.org/2023/formulas/mathematics/college/niovh55p0erasu4cogtap4ukbdw293veoh.png)
![undefined]()