Question

If the 18th term of the arithmetic sequence is 180, and the common difference is 10, find the 16th term of the sequence by using the recursive formula.140150160170

Answer 1

We are given an arithmetic sequence that has a common difference of 10 and the 18th term is 180.

We will use the recursive formula.

In an arithmetic sequence, we have that the nth term is given by:

`a_n=a_1+(n-1)d`

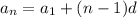
Where:

`\begin{gathered} a_n=nth\text{ term} \\ a_1=\text{ first term} \\ d=\text{ common difference} \end{gathered}`

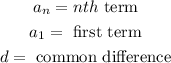
Since the 18th term is 180 we have that:

`a_(18)=180`

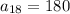
This means that when we substitute the value of "n" by 18 the result is 180:

`\begin{gathered} a_(18)=a_1+(18-1)(10) \\ \\ 180=a_1+(17)(10) \\ \\ 180=a_1+170 \end{gathered}`

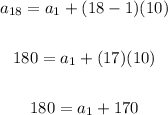
Now, we solve for the first term:

`\begin{gathered} 180-170=a_1 \\ 10=a_1 \end{gathered}`

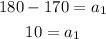
Now, we can apply the formula again using the first term:

`a_n=10+(n-1)(10)`

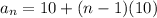
Now, we substitute the value of "n = 16";

`\begin{gathered} a_(16)=10+(16-1)(10) \\ \\ a_(16)=10+(15)(10) \\ \\ a_(16)=10+150 \\ \\ a_(16)=160 \end{gathered}`

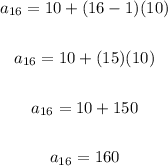
Therefore, the 16th term is 160