We are given an arithmetic sequence that has a common difference of 10 and the 18th term is 180.
We will use the recursive formula.
In an arithmetic sequence, we have that the nth term is given by:

Where:
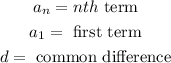
Since the 18th term is 180 we have that:
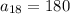
This means that when we substitute the value of "n" by 18 the result is 180:
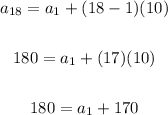
Now, we solve for the first term:
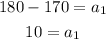
Now, we can apply the formula again using the first term:
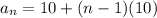
Now, we substitute the value of "n = 16";

Therefore, the 16th term is 160