Define the system of equations that describes the situation.
Take x as the number of quarters and y as the number of dimes, according to the question the total number of coins, which is the sum of quarter and dimes, is 28:
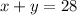
Also, using the equivalence in cents we know that each quarter is 25 cents and each dime is 10 cents. Expressed as dollars, a quarter equals 0.25 dollars and a dime equals 0.10 dollars. According to the question, the total amount of money is $5.05, this is the sum of the product of 0.25 and the number of quarters and the product of 0.10 and the number of dimes.:
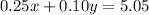
Use both equations to define the system of equations:
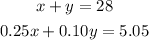
Use substitution to solve the system:
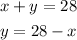
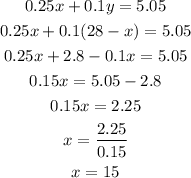
15 of the coins are quarters.