Question

2. How many years are needed for ₱40,000 to yield ₱13,755.66 interest if the interest rate is 6% compounded semi-annually?

Answer 1

We have that the formula for the compound interest semi annually is:

`A=P(1+(r)/(2))^(2t)`

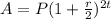
where A is the total amount, P is the principal amount, r is the interest rate and t is the time in years.

In this case, we have the following information:

`\begin{gathered} r=6\%=0.06 \\ A=40000+13755.66=53755.66 \\ P=40000 \end{gathered}`

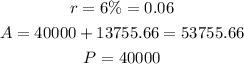
then, using the first equation, we get:

`\begin{gathered} 53755.66=40000(1+(0.06)/(2))^(2t) \\ \Rightarrow(53755.66)/(40000)=(1+0.03)^(2t) \\ \Rightarrow1.3439=(1.03)^(2t) \end{gathered}`

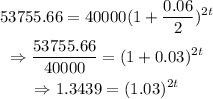
using logarithm on both sides of the equation, we get the following:

`\begin{gathered} \ln (1.3439)=\ln (1.03^(2t)) \\ \Rightarrow\ln (1.3439)=2t\ln (1.03) \\ \Rightarrow t=(\ln (1.3439))/(2\ln (1.03))=4.99\approx5 \\ t\approx5 \end{gathered}`

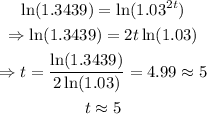
therefore, it wil take approximately 5 years to get the desired interest.